미분은 함수의 변화율을 분석하는 중요한 수학적 도구로 다양한 분야에서 널리 사용됩니다. 미적분학을 배우려면 미분 공식을 잘 이해하고 사용하는 것이 필수적입니다. 이번 글에서는 9가지 기본 미분 공식에 대해 자세히 설명하고, 각 공식의 의미와 응용 사례를 통해 이해를 돕겠습니다.

1. 상수 함수의 미분 공식: (frac{d}{dx}(c) = 0) 여기서 (c)는 상수입니다. 상수 함수의 도함수는 항상 0입니다. 이는 상수가 변하지 않기 때문에 기울기가 없다는 것을 의미합니다. 예:(f(x) = 5 쿼드 오른쪽 화살표 쿼드 f'(x) = 0)2. 거듭제곱 함수의 미분 공식:(frac{d}{dx}(x^n) = nx^{n-1})여기서 (n)은 실수입니다. 이 공식은 다항식 함수의 기본 미분 규칙이며 (x)의 거듭제곱에 대한 미분을 나타냅니다. 예:(f(x) = x^3 쿼드 오른쪽 화살표 쿼드 f'(x) = 3x^{2})3. 상수 배수에 대한 미분 공식:(frac{d}{dx}(c cdot f(x)) = c cdot f'(x))여기서 (c)는 상수이고 (f(x))는 미분 가능한 함수입니다. . . 상수를 곱한 함수의 도함수는 상수를 곱한 도함수를 유지합니다. 예: (f(x) = 4x^2 쿼드 Rightarrow 쿼드 f'(x) = 4 cdot (2x) = 8x)
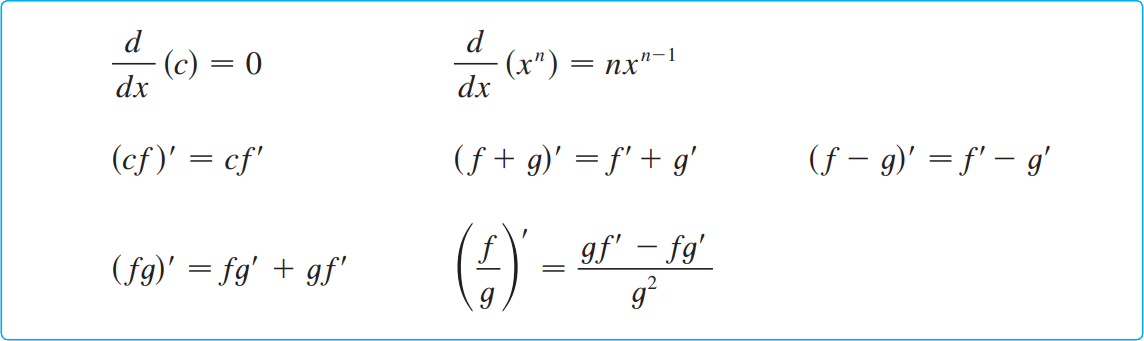
4. 합에 대한 미분 공식: (frac{d}{dx}(f(x) + g(x)) = f'(x) + g'(x)) 두 함수 합의 미분은 다음과 같습니다. 각 함수의 미분을 추가합니다. 똑같습니다. 이는 미분에 선형성이 있음을 나타냅니다. 예:(f(x) = x^2 + sin(x) 쿼드 오른쪽 화살표 쿼드 f'(x) = 2x + cos(x))5. 차이에 대한 미분 공식: (frac{d}{dx}(f(x) – g(x)) = f'(x) – g'(x)) 두 함수 간의 차이의 미분은 다음의 도함수를 빼서 수행됩니다. 각 기능. 똑같습니다. 이는 또한 차별화의 선형성을 나타냅니다. 예: (f(x) = e^x – x^3 쿼드 오른쪽 화살표 쿼드 f'(x) = e^x – 3x^2)

6. 곱의 미분 공식:(frac{d}{dx}(f(x) cdot g(x)) = f'(x)g(x) + f(x)g'(x)) 두 함수 곱의 도함수는 첫 번째 함수와 두 번째 함수의 도함수에 첫 번째 함수와 두 번째 함수의 도함수의 곱을 합한 것입니다. 이 공식을 곱의 법칙이라고 합니다. 예:(f(x) = x^2 쿼드 g(x) = sin(x) 쿼드 오른쪽 화살표 쿼드 f'(x)g(x) + f(x)g’ (x ) = 2x 죄(x) + x^2 cos(x))7. 몫의 미분 공식:(frac{d}{dx}left(frac{f(x)}{g(x)}right) = frac{f'(x)g(x) – f(x)g'( x)}{(g(x))^2})두 함수의 몫의 도함수는 분자의 도함수에 분모를 곱한 값이고, 분자의 함수에 분모의 도함수를 곱한 값은 다음과 같습니다. 빼서 그 결과를 분모로 나눕니다. 제곱으로 나누는 것과 같습니다. 이 공식을 몫의 법칙이라고 합니다.예:(f(x) = x^2 쿼드 g(x) = e^x 쿼드 오른쪽 화살표 쿼드 frac{d}{dx}left(frac{x^2}{e ^ x}오른쪽) = frac{2xe^x – x^2e^x}{(e^x)^2} = frac{(2x – x^2)e^x}{e^{2x}})8 . 삼각 함수의 미분 공식:(frac{d}{dx}(sin(x)) = cos(x))(frac{d}{dx}(cos(x)) = -sin(x))(frac{ d}{dx}(tan(x)) = sec^2(x)) 삼각 함수의 도함수는 각각 고유한 패턴을 갖습니다. 이는 주기적이며, 주기 함수의 미분을 통해 많은 실제 문제를 해결할 수 있습니다. 예: (f(x) = sin(x) 쿼드 오른쪽 화살표 쿼드 f'(x) = cos(x))
9. 지수 및 로그 함수의 미분 공식:(frac{d}{dx}(e^x) = e^x)(frac{d}{dx}(a^x) = a^x ln(a) ) (여기서 (a > 0))(frac{d}{dx}(log_a(x)) = frac{1}{x ln(a)})지수 및 로그 함수의 경우 미분은 매우 유용한. , 다양한 수학적 모델에 나타납니다. 예:(f(x) = e^x 쿼드 오른쪽 화살표 쿼드 f'(x) = e^x)(g(x) = log(x) 쿼드 오른쪽 화살표 쿼드 g'(x ) = frac{1 }{x}) 결론 위에서 살펴본 9개의 미분 공식은 미적분학의 기초를 형성하는 중요한 개념입니다. 이러한 공식은 함수의 성질을 분석하고 다양한 문제를 해결하는 데 필수적입니다.
#수학공부#미분공식